Оба очень хорошие предложения - спасибо, что нашли время, чтобы поделиться! Я уверен, что будет осуществлять это.
Отличная идея!
Два предложения:
1) [...] если вы технически открыть цветок один раз каждые 24 часа (не связанные с Calender дней), что может привести к 2 отверстия на один календарный день [...] В результате Вы можете сказать, что цветок открывает "как минимум" один раз в день [...]
Нет, это не является точным, и критический ум будет совершенно верно с учетом этого сомнительна.
Если ввести случайное время Т между двумя отверстиями, где T составляет в среднем 24 часов, вы будете иметь в среднем на 1 отверстие в день, а в среднем 365 открываний в год и т.д. НО: Вы можете (! И) очень хорошо иметь периоды времени более 24 часов, тоже, то есть вы будете иметь календарных дней (а иногда даже два или более последовательных календарных дней) без открытия вообще.
Таким образом, это просто
не правильно утверждать, "что цветок открывает "как минимум" один раз в день".
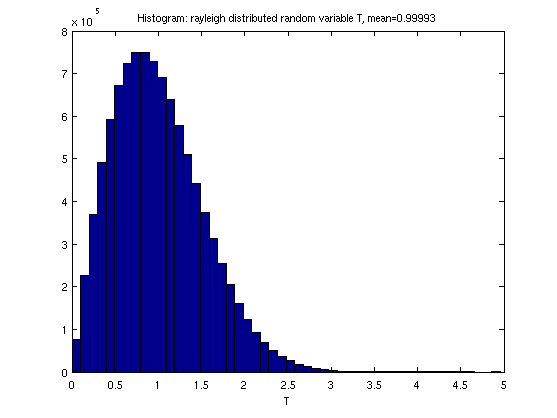
Вот быстрый пример, при осуществлении времени Т как случайная величина следующего распределения Рэлея, со средним значением Т = 1,0 дней:
Matlab код:
>> N = 1e7; х = randn (1, N); у = randn (1, N); (. Х ^ 2 + у ^ 2.) Т = SQRT / SQRT (пи / 2); му = среднее (Т),
>> Hist (Т, 50); Название ([ 'Гистограмма: Рэлея распределенная случайная величина Т, означают =', num2str (мю)]); xlabel ( 'Т')
>> 100 * Длина (Т (Т<0,90)) / длина (Т), 100 * Длина (Т (Т<0,50)) / длина (Т), 100 * Длина (Т (Т<0,25)) / Длина (Т)
>> 100 * Длина (Т (Т>1,0)) / Длина (Т), 100 * Длина (Т (Т>1.5)) / длина (Т), 100 * Длина (Т (Т>2.0)) / Длина (Т)
Результат:
* В 47,1% / 17,8% / 4,8% от всех случаев, продолжительность времени Т между двумя отверстиями короче, чем 0,90 / 0,50 / 0,25 дней
Но также:
* В 45,6% / 17,1% / 4,3% от всех случаев, продолжительность времени Т между двумя отверстиями больше, чем 1.0 / 1.5 / 2.0 дней
Re: Таинственный Bitcoin цветок открывает один раз в день и открывает свободный Bitcoin
